Creating Boresch Restraints for ABFE Calculations (Tyk2)
Learning objectives
Learn how to determine Boresch restraints from end-state trajectories.
Relevant literature
Coming Soon!
Tutorial
In this Tutorial, you will learn how to create Boresch restraints for use in Absolute Binding Free Energy (ABFE) calculations using the Tyk2 system as an example.
Determining Boresch Restraints
For this tutorial, we will be starting from the equilibrated end-state trajectory of a Tyk2-ligand complex in its bound state. These files were generated in the tutorial:ref:Equilibrating the End States of Tyk2 for ABFE Calculations <build_binder>; however, for convenience we have provided the necessary files below to get you started.
Attention
Update the download link to point to the finalized tutorial files once they are uploaded.
Theory of Boresch Restraints
Boresch restraints are a type of positional restraint used in molecular dynamics simulations to maintain the relative position and orientation of a ligand within a binding site. They are particularly useful in absolute binding free energy calculations, where it is essential to keep the ligand in place while decoupling its interactions with the environment.
The Boresch restraint method involves defining a set of six restraints based on three atoms from the ligand and three atoms from the protein. These restraints include:
One distance Restraint
Two Angle Restraints
Three Dihedral Restraints
These restraints work together to fix the ligand’s position and orientation relative to the protein, allowing for accurate free energy calculations.
Note
This theory section should be expanded with a more detailed explanation of the mathematical formulation of Boresch restraints, including equations and diagrams to illustrate the concepts.
Note
Much of the below theoretical discussion comes from Boresch et al., J. Phys. Chem. B, 2003, 107 (35), pp 9535–9551. DOI: 10.1021/jp0217839.
The goal of Boresch restraints is to define a known set of lambda-dependent restraints that can be applied to the ligand in the bound state to keep it in place while decoupling its interactions with the environment, while also allowing for an analytical correction to the free energy to account for the restraints.
Roughly, the situation that needs to be corrected for is:
Where here, (P cdot L)_{H_2O} is the protein-ligand complex in water with restraints applied, (P)_{H_2O} is the protein in water, and (L)_{H_2O} is the ligand in water. $Delta A_r$ is the free energy change associated with removing the restraints from the complex in water.
Because the ligand is in the dummy state when decoupled, the Ligand does not have interactions with the protein or solvent and thus the restraints are the only interactions with external sources it feels. The potential energy function for the system is:
Here, there are terms coming from the protein (\(U_P\)), the ligand (\(U_L\)), and the restraints (\(U_r\)).
The contribution to the free energy that comes from the restraints can be written as:
Where \(Z_{P \cdot L}\) is the partition function of the restrained complex, \(Z_P\) is the partition function of the protein, and \(Z_L\) is the partition function of the ligand.
This calculation is feasible analytically when the restraints are chosen such that
or in other words, choosing the restraints such that the partition function can be factored into independent contributions from the protein, ligand, and restraints.
After a few assumptions (Rigid Rotor) the final expression for the partition function is given by:
Finally, the free energy contribution from the restraints can be expressed as:
Where \(r_{aA,0}\) and \(\theta_{A,0}\) are the equilibrium distance and angle values for the restraints, and \(K_r\), \(K_{\theta^A}\), \(K_{\theta^B}\), \(K_{\phi^A}\), \(K_{\phi^B}\), and \(K_{\phi^C}\) are the force constants for the respective restraints.
How to Determine Boresch Restraints
To determine the Boresch restraints for your system, you will need to analyze an equilibrated trajectory for the protein-ligand complex.
Note
If you have been following along with the Tyk2 ABFE Tutorials, it is very likely that you have already generated a trajectory. It very likely that your trajectory will be different from the one included here, but the steps to generate the boresch restraints will be the same. Don’t be surprised if your final results differ from those presented here!
For this tutorial, we will be using the following python code, which you should save as generate_boresch_restraints.py:
#!/usr/bin/env python3
"""Generate Boresch restraints from equilibration trajectory.
This script scans ligand heavy atoms and nearby protein heavy atoms to
identify stable anchor pairs, computes Boresch degrees of freedom over
the trajectory, and prints/writes restraint parameters.
Behavior is preserved from the original script but reorganized for
readability and reuse.
"""
import argparse
import logging
from pathlib import Path
import MDAnalysis as mda
from MDAnalysis.analysis.distances import dist
from MDAnalysis.lib.distances import calc_dihedrals
import numpy as np
from numpy.linalg import norm
import matplotlib.pyplot as plt
LOG = logging.getLogger(__name__)
def parse_args():
"""Parse command-line arguments.
Returns
-------
argparse.Namespace
Object with attributes:
- topology: str, path to topology file (default './unisc.parm7')
- trajectory: str, path to trajectory file (default 'equil1/real_eq.nc')
- ligand_sel: str, MDAnalysis selection string for ligand heavy atoms
- cutoff: float, distance in angstroms to search for nearby protein atoms
- num_pairs: int, number of lowest-standard-deviation pairs to show/select
- max_pairs_traj: int, maximum number of pairs to analyze over the trajectory
- out_rest: str, output filename to write AMBER restraint input
- fig_prefix: str, prefix for any figures written
Notes
-----
This function only constructs and returns the parsed arguments object.
Documentation in tutorials should show running the script like:
$ python generate_boresch_restraints.py --topology my.parm7 --trajectory my.nc
"""
p = argparse.ArgumentParser(
description="Generate Boresch restraints from equilibration trajectory"
)
p.add_argument("--topology", type=str, default="./unisc.parm7", help="Topology file")
p.add_argument("--trajectory", type=str, default="equil1/real_eq.nc", help="Equilibration trajectory file")
p.add_argument("--ligand-sel", type=str, default="resid 1 and not name H*", help="Selection for ligand heavy atoms")
p.add_argument("--cutoff", type=float, default=10.0, help="Cutoff (angstrom) to search nearby protein atoms")
p.add_argument("--num-pairs", type=int, default=5, help="Number of low-SD pairs to show/select")
p.add_argument("--max-pairs-traj", type=int, default=200, help="Max pairs to analyze over trajectory")
p.add_argument("--out-rest", type=str, default="rest.in", help="Output restraint file")
p.add_argument("--fig-prefix", type=str, default="boresch", help="Prefix for saved figures")
return p.parse_args()
def find_anchor_pairs(u, ligand_sel="resid 1 and not name H*", cutoff=10.0):
"""Find candidate ligand-protein anchor atom pairs.
Parameters
----------
u : MDAnalysis.Universe
Loaded universe containing topology and trajectory.
ligand_sel : str
MDAnalysis selection string identifying ligand heavy atoms (no H).
cutoff : float
Distance cutoff (in Å) used to find protein heavy atoms near each
ligand heavy atom.
Returns
-------
dict
Mapping (ligand_atom_index, protein_atom_index) -> dict with key
'dists' initialized to an empty list. Distances over the trajectory
will be appended to this list by :func:`collect_distances`.
Behavior details
----------------
- Protein atoms are selected with the MDAnalysis "around" syntax.
- The returned atom indices are MDAnalysis global atom indices (0-based).
"""
lig_heavy = u.select_atoms(ligand_sel)
anchors = {}
for lig_atom in lig_heavy:
# select protein heavy atoms within cutoff of ligand atom
prot_sel = f"(protein or resname PRT) and (around {cutoff} index {lig_atom.index}) and (not name H*)"
prot_atoms = u.select_atoms(prot_sel)
for prot_atom in prot_atoms:
anchors[(lig_atom.index, prot_atom.index)] = {"dists": []}
return anchors
def collect_distances(u, anchors):
"""Populate `anchors` with distance time series from the trajectory.
Parameters
----------
u : MDAnalysis.Universe
Universe that has already been loaded with topology and trajectory.
anchors : dict
Dictionary produced by :func:`find_anchor_pairs`. Keys are (lig_idx, prot_idx).
Returns
-------
dict
The same anchors dict with 'dists' converted to numpy arrays and
augmented with 'avg_dist' and 'sd_dist' for each pair.
Notes
-----
- Distances are computed frame-by-frame using MDAnalysis distance routines
with periodic box handling (box=frame.dimensions).
- For performance, this function iterates over frames and pairs; for large
trajectories or many pairs consider vectorized approaches or sampling.
"""
# Iterate trajectory and collect distances for each pair
for frame in u.trajectory:
for lig_idx, prot_idx in list(anchors.keys()):
# compute distance using MDAnalysis distance routine
distance = dist(
mda.AtomGroup([u.atoms[lig_idx]]),
mda.AtomGroup([u.atoms[prot_idx]]),
box=frame.dimensions,
)[2][0]
anchors[(lig_idx, prot_idx)]["dists"].append(distance)
# convert lists to numpy arrays and compute stats
for pair in anchors.keys():
anchors[pair]["dists"] = np.array(anchors[pair]["dists"])
anchors[pair]["avg_dist"] = anchors[pair]["dists"].mean()
anchors[pair]["sd_dist"] = anchors[pair]["dists"].std()
return anchors
def report_low_sd_pairs(u, anchors, n=5):
"""Report and return the top-N anchor pairs with lowest distance SD.
Parameters
----------
u : MDAnalysis.Universe
Universe used only for pretty-printing atom information.
anchors : dict
Anchors dict returned by :func:`collect_distances`.
n : int
Number of pairs to report.
Returns
-------
list
Ordered list of (lig_idx, prot_idx) tuples sorted by ascending SD.
This function logs informative lines that can be included in a tutorial
to show how candidate anchor pairs are selected based on stability.
"""
ordered = [item[0] for item in sorted(anchors.items(), key=lambda it: it[1]["sd_dist"]) ]
LOG.info("Top %d pairs by lowest SD:", n)
for i, pair in enumerate(ordered[:n]):
a, b = pair
LOG.info("Pair %d: %s - avg %.2f SD %.2f", i + 1, (u.atoms[a], u.atoms[b]), anchors[pair]["avg_dist"], anchors[pair]["sd_dist"])
return ordered
def get_anchor_ats(a1_idx, u):
"""Select three anchor atoms around a given atom index.
Parameters
----------
a1_idx : int
Index of the primary anchor atom (0-based, MDAnalysis indexing).
u : MDAnalysis.Universe
Universe containing topology information - used to query bonded atoms.
Returns
-------
tuple
(a1_idx, a2_idx, a3_idx) where a2 and a3 are heavy atoms chosen to be
bonded neighbors of a1 (or the next atoms along the chain if at a terminus).
Behavior and edge cases
-----------------------
- The function prefers bonded heavy atoms that are not hydrogens.
- If a1 is terminal (only a single heavy neighbor), the function walks
one more bond along that neighbor to find a3.
- If no bonded heavy atoms are found an exception is raised; calling
code should ensure anchor candidates are sensible (heavy atoms typically have bonded neighbors).
Rationale
---------
These three anchor atoms are used to define internal angles/dihedrals
in Boresch-style restraints: the ligand anchor (a1,a2,a3) will be paired
with a receptor anchor triplet to define distance/angle/dihedral restraints.
"""
a1_at = u.atoms[a1_idx]
# select bonded heavy atoms (not hydrogens)
bonded_heavy = a1_at.bonded_atoms.select_atoms("not name H*")
if len(bonded_heavy) == 0:
raise RuntimeError(f"No bonded heavy atoms found for atom index {a1_idx}")
a2_idx = bonded_heavy[0].index
if len(bonded_heavy) > 1:
a3_idx = bonded_heavy[1].index
else:
# step one further away along heavy atoms
next_heavy = bonded_heavy[0].bonded_atoms.select_atoms("not name H*")
# prefer the second atom if that avoids going back to a1_idx
a3_candidate = next_heavy[1].index if len(next_heavy) > 1 else next_heavy[0].index
if a3_candidate == a1_idx and len(next_heavy) > 1:
a3_candidate = next_heavy[0].index
a3_idx = a3_candidate
return a1_idx, a2_idx, a3_idx
# Geometry helpers
def get_distance(idx1, idx2, u):
"""Compute Euclidean distance (Å) between two atoms by index.
Parameters
----------
idx1, idx2 : int
Atom indices (0-based).
u : MDAnalysis.Universe
Returns
-------
float
Distance in Å.
"""
return dist(mda.AtomGroup([u.atoms[idx1]]), mda.AtomGroup([u.atoms[idx2]]), box=u.dimensions)[2][0]
def get_angle(idx1, idx2, idx3, u):
"""Compute angle (radians) defined by three atoms A-B-C.
Parameters
----------
idx1 : int
Index of atom C (first argument in original function definition)
idx2 : int
Index of atom B (central atom)
idx3 : int
Index of atom A (last argument)
u : MDAnalysis.Universe
Returns
-------
float
Angle in radians.
Notes
-----
The ordering follows the original script: get_angle(idx1, idx2, idx3)
returns the angle at atom idx2 formed by vectors (A-B) and (C-B) where
A = idx3, B = idx2, C = idx1.
"""
C = u.atoms[idx1].position
B = u.atoms[idx2].position
A = u.atoms[idx3].position
BA = A - B
BC = C - B
angle = np.arccos(np.dot(BA, BC) / (norm(BA) * norm(BC)))
return angle
def get_dihedral(idx1, idx2, idx3, idx4, u):
"""Compute dihedral (torsion) angle in radians for four atoms.
Parameters
----------
idx1, idx2, idx3, idx4 : int
Atom indices specifying the torsion in the order used by MDAnalysis.
u : MDAnalysis.Universe
Returns
-------
float
Dihedral angle in radians (range -pi..pi).
Notes
-----
MDAnalysis' calc_dihedrals returns values in the range (-pi, pi].
"""
positions = [u.atoms[idx].position for idx in [idx1, idx2, idx3, idx4]]
dihedral = calc_dihedrals(positions[0], positions[1], positions[2], positions[3], box=u.dimensions)
return dihedral
def get_boresch_dof(l1, l2, l3, r1, r2, r3, u):
"""Compute the Boresch degrees of freedom for a given anchor sextet.
Parameters
----------
l1,l2,l3 : int
Indices of the three ligand anchor atoms (l1 is bonded to receptor r1).
r1,r2,r3 : int
Indices of the three receptor anchor atoms (r1 bonded to ligand l1).
u : MDAnalysis.Universe
Returns
-------
tuple
(r, thetaA, thetaB, phiA, phiB, phiC, thetaR, thetaL)
Where
-----
- r : float, distance between r1 and l1 (Å)
- thetaA, thetaB : floats, angles (radians)
- phiA, phiB, phiC : floats, dihedrals (radians)
- thetaR, thetaL : internal receptor/ligand angles (radians)
Usage
-----
These values correspond to the common variables used to define a set
of Boresch restraints (one distance, two angles, three dihedrals).
"""
# Ordering r3,r2,r1,l1,l2,l3 as in original
r = get_distance(r1, l1, u)
thetaA = get_angle(r2, r1, l1, u)
thetaB = get_angle(r1, l1, l2, u)
phiA = get_dihedral(r3, r2, r1, l1, u)
phiB = get_dihedral(r2, r1, l1, l2, u)
phiC = get_dihedral(r1, l1, l2, l3, u)
thetaR = get_angle(r3, r2, r1, u)
thetaL = get_angle(l1, l2, l3, u)
return r, thetaA, thetaB, phiA, phiB, phiC, thetaR, thetaL
def analyze_boresch_over_traj(u, pairs, max_pairs=200):
"""Compute time series and statistics for Boresch DOF across trajectory.
Parameters
----------
u : MDAnalysis.Universe
Universe with trajectory.
pairs : iterable
Iterable of (l1_idx, r1_idx) anchor pairs to analyze.
max_pairs : int
Maximum number of pairs to process (for performance control).
Returns
-------
dict
Mapping pair -> dict with keys:
- 'anchor_ats': [l1,l2,l3,r1,r2,r3]
- for each dof e.g. 'r', 'phiA', etc.: dict with 'values' (np.array), 'avg', 'sd', 'k'
- 'tot_var': sum of variances used to rank pair suitability
Important details
-----------------
- For dihedral DOFs (phiA/B/C) this function applies a circular-statistics
aware procedure to compute mean and standard deviation so that periodicity
is correctly handled (angles near -pi and +pi are treated continuously).
- Force constants k are estimated assuming a Gaussian distribution via
k = RT / sd^2, where RT is approximated as 0.593 kcal/mol at 289 K in
the original script. This is the same convention and will be halved
later when writing restraint parameters to be consistent with external tools.
"""
boresch = {}
boresch_dof_list = ["r", "thetaA", "thetaB", "phiA", "phiB", "phiC", "thetaR", "thetaL"]
for pair in pairs[:max_pairs]:
boresch[pair] = {}
l1_idx, r1_idx = pair
_, l2_idx, l3_idx = get_anchor_ats(l1_idx, u)
_, r2_idx, r3_idx = get_anchor_ats(r1_idx, u)
boresch[pair]["anchor_ats"] = [l1_idx, l2_idx, l3_idx, r1_idx, r2_idx, r3_idx]
for dof in boresch_dof_list:
boresch[pair][dof] = {"values": []}
n_frames = len(u.trajectory)
for i, frame in enumerate(u.trajectory):
r, thetaA, thetaB, phiA, phiB, phiC, thetaR, thetaL = get_boresch_dof(
l1_idx, l2_idx, l3_idx, r1_idx, r2_idx, r3_idx, u
)
boresch[pair]["r"]["values"].append(r)
boresch[pair]["thetaA"]["values"].append(thetaA)
boresch[pair]["thetaB"]["values"].append(thetaB)
boresch[pair]["phiA"]["values"].append(phiA)
boresch[pair]["phiB"]["values"].append(phiB)
boresch[pair]["phiC"]["values"].append(phiC)
boresch[pair]["thetaR"]["values"].append(thetaR)
boresch[pair]["thetaL"]["values"].append(thetaL)
# After frames loop compute statistics
boresch[pair]["tot_var"] = 0.0
for dof in boresch_dof_list:
values = np.array(boresch[pair][dof]["values"])
boresch[pair][dof]["values"] = values
avg = values.mean()
boresch[pair][dof]["avg"] = avg
if dof.startswith("phi"):
# circular statistics handling for dihedrals
corrected_vals = []
for val in values:
dtheta = abs(val - avg)
corrected_vals.append(min(dtheta, 2 * np.pi - dtheta))
corrected_vals = np.array(corrected_vals)
boresch[pair][dof]["sd"] = corrected_vals.std()
# correct mean
periodic_bound = avg - np.pi
if periodic_bound < -np.pi:
periodic_bound += 2 * np.pi
corrected_avg_vals = [v + 2 * np.pi if v < periodic_bound else v for v in values]
m_corr = np.array(corrected_avg_vals).mean()
if m_corr > np.pi:
boresch[pair][dof]["avg"] = m_corr - 2 * np.pi
else:
boresch[pair][dof]["avg"] = m_corr
else:
boresch[pair][dof]["sd"] = values.std()
if dof not in ("thetaR", "thetaL"):
boresch[pair]["tot_var"] += boresch[pair][dof]["sd"] ** 2
boresch[pair][dof]["k"] = 0.593 / (boresch[pair][dof]["sd"] ** 2)
return boresch
def select_pairs(boresch_dict):
"""Select suitable anchor pairs based on geometric filters.
Parameters
----------
boresch_dict : dict
Output from :func:`analyze_boresch_over_traj`.
Returns
-------
list
Filtered list of pairs, ordered by increasing tot_var.
Filtering criteria
------------------
- Distance r average must be > 1.0 Å (filters out extremely close/invalid pairs)
- Average angles thetaA and thetaB must be within (0.52, 2.62) radians (~30°-150°)
These thresholds were chosen empirically to avoid degenerate restraints.
"""
# order by tot_var
ordered = [item[0] for item in sorted(boresch_dict.items(), key=lambda it: it[1]["tot_var"]) ]
# filter by distance and internal angles
selected = []
for pair in ordered:
cond_dist = boresch_dict[pair]["r"]["avg"] > 1.0
avg_angles = [boresch_dict[pair][a]["avg"] for a in ("thetaA", "thetaB")]
cond_angles = all((0.52 < ang < 2.62) for ang in avg_angles)
if cond_dist and cond_angles:
selected.append(pair)
return selected
def plot_time_series(boresch_dict, pairs, fig_prefix="boresch", num_pairs=5):
"""Plot time series for each Boresch DOF for the top candidate pairs.
The plotting function will unwrap phi (dihedral) time series around the
computed circular mean so that the plot does not show large jumps at the
-π/π periodic boundary. Figures are saved with the prefix provided.
Parameters
----------
boresch_dict : dict
Boresch results as produced by :func:`analyze_boresch_over_traj`.
pairs : list
Candidate pairs (ordering is preserved); only the first `num_pairs`
are plotted.
fig_prefix : str
Prefix used for saved figure filenames.
num_pairs : int
Number of pairs to include in the plot (default 5).
"""
dofs = ["r", "thetaA", "thetaB", "phiA", "phiB", "phiC", "thetaR", "thetaL"]
n_dof = len(dofs)
fig, axs = plt.subplots(1, n_dof, figsize=(2.6 * n_dof, 6))
def _unwrap_to_mean(values, mean):
"""Shift angular values by multiples of 2*pi so they lie within (mean-pi, mean+pi]."""
return mean + ((values - mean + np.pi) % (2 * np.pi) - np.pi)
for i, dof in enumerate(dofs):
for j, pair in enumerate(list(boresch_dict.keys())[:num_pairs]):
vals = boresch_dict[pair][dof]["values"]
# For dihedrals (phi) unwrap values around their mean to avoid jumps at the -pi/pi boundary
if dof.startswith("phi"):
mean = boresch_dict[pair][dof].get("avg", 0.0)
vals_plot = _unwrap_to_mean(vals, mean)
else:
vals_plot = vals
axs[i].plot(np.arange(len(vals_plot)), vals_plot, label=f"Pair {pair}")
axs[i].set_xlabel("Frame No")
axs[i].set_ylabel("r (\u212B)" if dof == "r" else f"{dof} (rad)")
axs[i].legend()
fig.tight_layout()
fig_file = f"{fig_prefix}_timeseries.png"
fig.savefig(fig_file)
LOG.info("Saved time series figure to %s", fig_file)
def plot_histograms(boresch_dict, pairs, fig_prefix="boresch", highlight_pairs=None):
"""Plot histograms of DOF distributions for top candidate pairs.
Parameters
----------
boresch_dict : dict
Boresch data structure.
pairs : list
Candidate pairs selected for plotting.
fig_prefix : str
Prefix for saved histogram images.
Notes
-----
- Histograms include a vertical dashed line showing the computed average.
- Dihedral values are plotted in their stored range (after circular
averaging), which avoids misleading binning across the -π/π boundary.
"""
chosen = pairs[:3]
dof_order = ["r", "thetaA", "thetaB", "phiA", "phiB", "phiC"]
fig, axs = plt.subplots(len(chosen), len(dof_order), figsize=(16, 4 * len(chosen)))
for pi, pair in enumerate(chosen):
for di, dof in enumerate(dof_order):
ax = axs[pi][di] if len(chosen) > 1 else axs[di]
vals = boresch_dict[pair][dof]["values"]
# draw histogram and get patch artists so we can outline selected pairs
n, bins, patches = ax.hist(vals, bins=10)
ax.axvline(x=boresch_dict[pair][dof]["avg"], color="r", linestyle="dashed", linewidth=2)
# If this pair is in the highlight set, outline the bars and add title
if highlight_pairs and pair in highlight_pairs:
for p in patches:
p.set_edgecolor('red')
p.set_linewidth(1.2)
p.set_alpha(0.6)
ax.set_title(f"Selected pair: {pair}")
ax.set_xlabel("r (\u212B)" if dof == "r" else f"{dof} (rad)")
ax.set_ylabel("Num Vals")
fig.tight_layout()
fig_file = f"{fig_prefix}_histograms.png"
fig.savefig(fig_file)
LOG.info("Saved histogram figure to %s", fig_file)
def print_boresch_params(pair, boresch_dict, out_rest="rest.in"):
"""Write out restraint parameters for a chosen anchor pair.
Parameters
----------
pair : tuple
Anchor pair tuple returned by selection routines.
boresch_dict : dict
Results structure from :func:`analyze_boresch_over_traj`.
out_rest : str
Output filename for the AMBER restraint file (default 'rest.in').
Behavior
--------
- Prints a JSON-like single-line summary to stdout suitable for parsing
by tutorial readers or downstream tools.
- Writes an AMBER &rst formatted restraint file where atom indices are
converted to AMBER's 1-based indexing.
- Force constants are halved in the output to match the energy definition
used by some external MD codes (consistent with the original script).
"""
l1, l2, l3, r1, r2, r3 = boresch_dict[pair]["anchor_ats"]
r0 = boresch_dict[pair]["r"]["avg"]
thetaA0 = boresch_dict[pair]["thetaA"]["avg"]
thetaB0 = boresch_dict[pair]["thetaB"]["avg"]
phiA0 = boresch_dict[pair]["phiA"]["avg"]
phiB0 = boresch_dict[pair]["phiB"]["avg"]
phiC0 = boresch_dict[pair]["phiC"]["avg"]
kr = boresch_dict[pair]["r"]["k"] / 2
kthetaA = boresch_dict[pair]["thetaA"]["k"] / 2
kthetaB = boresch_dict[pair]["thetaB"]["k"] / 2
kphiA = boresch_dict[pair]["phiA"]["k"] / 2
kphiB = boresch_dict[pair]["phiB"]["k"] / 2
kphiC = boresch_dict[pair]["phiC"]["k"] / 2
json_str = (
'{"anchor_points":{"r1":%d, "r2":%d, "r3":%d, "l1":%d, "l2":%d, "l3":%d},'
'"equilibrium_values":{"r0":%.2f, "thetaA0":%.2f, "thetaB0":%.2f, "phiA0":%.2f, "phiB0":%.2f, "phiC0":%.2f},'
'"force_constants":{"kr":%.2f, "kthetaA":%.2f, "kthetaB":%.2f, "kphiA":%.2f, "kphiB":%.2f, "kphiC":%.2f}}'
) % (r1, r2, r3, l1, l2, l3, r0, thetaA0, thetaB0, phiA0, phiB0, phiC0, kr, kthetaA, kthetaB, kphiA, kphiB, kphiC)
print(json_str)
# write AMBER restraint input (indices are 1-based in AMBER)
with open(out_rest, "w") as fh:
fh.write(f"&rst iat={r1+1},{l1+1},0\n")
fh.write(f" r1={0.0:.5f},r2={r0:.5f},r3={r0:.5f},r4=999.000,rk2={kr:.2f}, rk3={kr:.2f}/\n")
fh.write(f"&rst iat={r2+1},{r1+1},{l1+1},0\n")
fh.write(f" r1={-180.0:.5f},r2={np.degrees(thetaA0):.5f},r3={np.degrees(thetaA0):.5f},r4=180.000,rk2={kthetaA:.2f}, rk3={kthetaA:.2f}/\n")
fh.write(f"&rst iat={r1+1},{l1+1},{l2+1},0\n")
fh.write(f" r1={-180.0:.5f},r2={np.degrees(thetaB0):.5f},r3={np.degrees(thetaB0):.5f},r4=180.000,rk2={kthetaB:.2f}, rk3={kthetaB:.2f}/\n")
fh.write(f"&rst iat={r3+1},{r2+1},{r1+1},{l1+1},0\n")
fh.write(f" r1={-180.0:.5f},r2={np.degrees(phiA0):.5f},r3={np.degrees(phiA0):.5f},r4=180.000,rk2={kphiA:.2f}, rk3={kphiA:.2f}/\n")
fh.write(f"&rst iat={r2+1},{r1+1},{l1+1},{l2+1},0\n")
fh.write(f" r1={-180.0:.5f},r2={np.degrees(phiB0):.5f},r3={np.degrees(phiB0):.5f},r4=180.000,rk2={kphiB:.2f}, rk3={kphiB:.2f}/\n")
fh.write(f"&rst iat={r1+1},{l1+1},{l2+1},{l3+1},0\n")
fh.write(f" r1={-180.0:.5f},r2={np.degrees(phiC0):.5f},r3={np.degrees(phiC0):.5f},r4=180.000,rk2={kphiC:.2f}, rk3={kphiC:.2f}/\n")
LOG.info("Wrote restraint file %s", out_rest)
def main():
"""Main driver for the script.
Loads the universe, identifies candidate anchor pairs, computes statistics,
selects suitable pairs, writes restraint input, and saves diagnostic figures.
This function orchestrates the overall workflow and emits informative
logging messages for tutorial users to follow along.
"""
args = parse_args()
logging.basicConfig(level=logging.INFO, format="%(asctime)s - %(levelname)s - %(message)s")
u = mda.Universe(args.topology, args.trajectory)
LOG.info("Loaded universe: %s, trajectory frames: %d", args.topology, len(u.trajectory))
anchors = find_anchor_pairs(u, ligand_sel=args.ligand_sel, cutoff=args.cutoff)
if not anchors:
LOG.error("No candidate anchors found. Adjust ligand selection or cutoff.")
return
anchors = collect_distances(u, anchors)
ordered_pairs = report_low_sd_pairs(u, anchors, n=args.num_pairs)
# Analyze boresch degrees of freedom over trajectory for top pairs
boresch = analyze_boresch_over_traj(u, ordered_pairs, max_pairs=args.max_pairs_traj)
# Order by variance and select suitable pairs
pairs_by_var = [item[0] for item in sorted(boresch.items(), key=lambda it: it[1]["tot_var"]) ]
LOG.info("Pairs ordered by tot_var (top 10): %s", pairs_by_var[:10])
selected = select_pairs(boresch)
LOG.info("Selected pairs after filtering: %s", selected)
if selected:
# plot and write restraints for the first selected pair
plot_time_series(boresch, selected, fig_prefix=args.fig_prefix, num_pairs=args.num_pairs)
plot_histograms(boresch, selected, fig_prefix=args.fig_prefix, highlight_pairs=selected)
print_boresch_params(selected[0], boresch, out_rest=args.out_rest)
else:
LOG.warning("No suitable pairs found after filtering. Increase candidates or relax filters.")
if __name__ == "__main__":
main()
This code uses the MDAnalysis package to analyze the trajectory and select appropriate atoms for the Boresch restraints.
You can run the code with the following command:
python generate_boresch_restraints.py
This will create a couple of image files, as well as a “rest.in” file that contains the necessary restraint information for use in an Amber simulation.
There are two image files that are generated by the script.
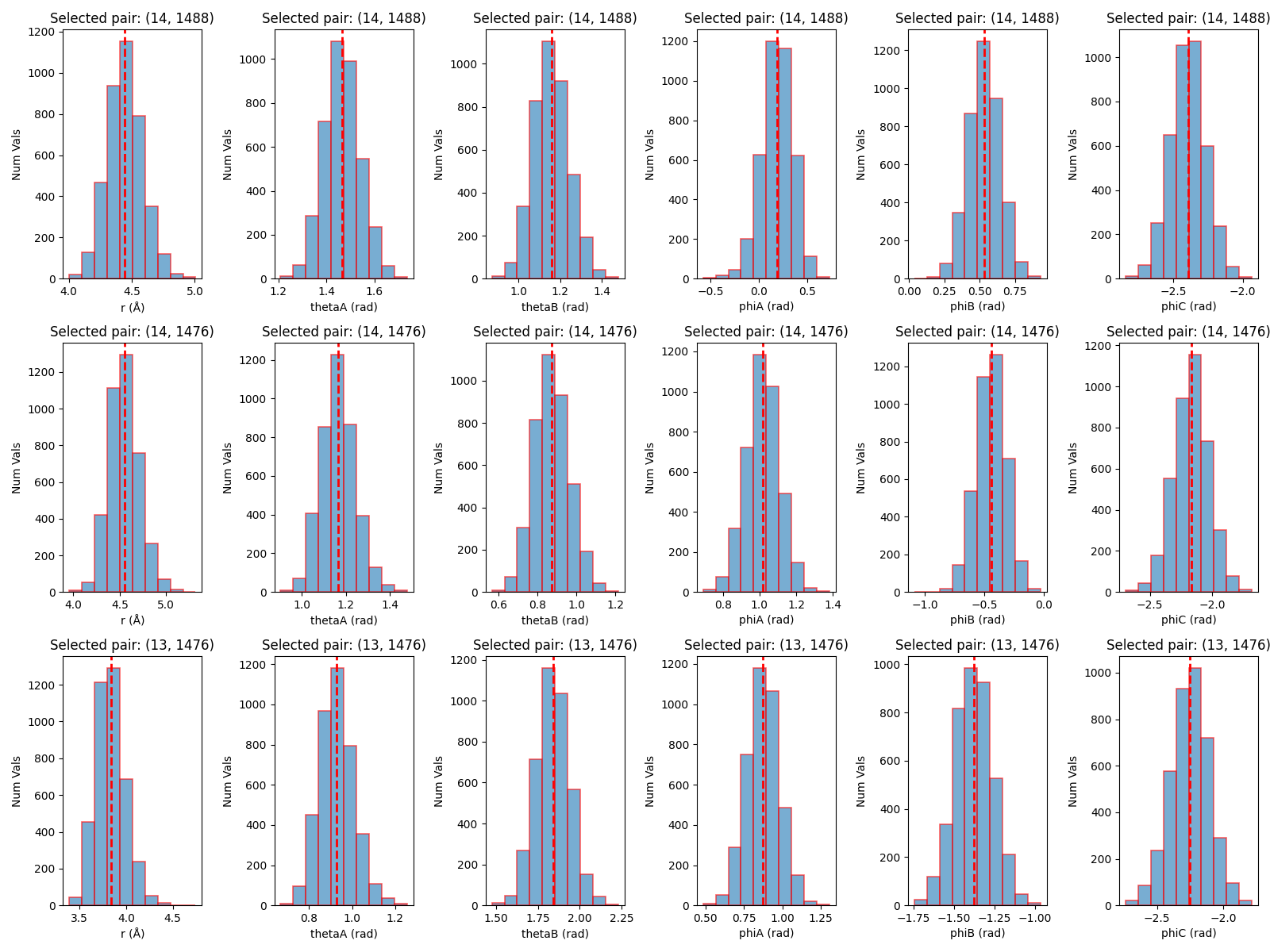
The first is boresch_histograms.png, which shows the histograms of the distance, angle, and dihedral values for the selected atoms over the course of the trajectory. This is useful for visualizing how well the selected atoms maintain their relative positions and orientations.
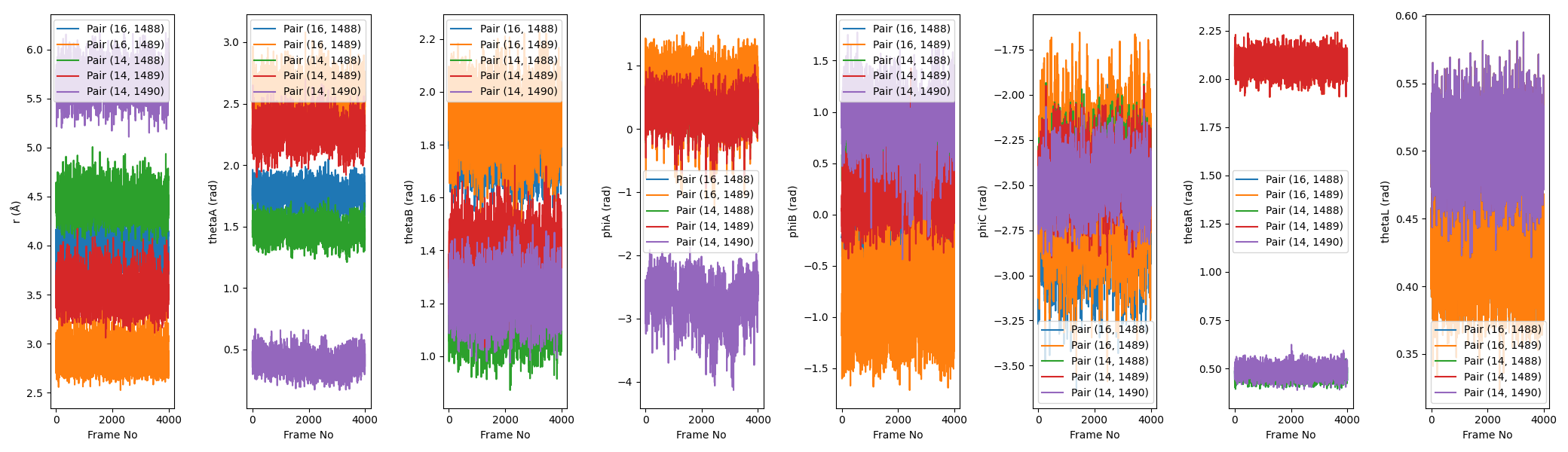
The second image is boresch_timeseries.png, which shows the time series of the distance, angle, and dihedral values for the selected atoms over the course of the trajectory. This is useful for visualizing how stable the selected atoms are over time.
The final output is the rest.in file, which contains the necessary restraint information for use in an Amber simulation. This file includes the atom indices, equilibrium values, and force constants for the Boresch restraints.
An example of the rest.in file generated is shown below:
&rst iat=1489,15,0
r1=0.00000,r2=4.44575,r3=4.44575,r4=999.000,rk2=15.06, rk3=15.06/
&rst iat=1477,1489,15,0
r1=-180.00000,r2=83.99734,r3=83.99734,r4=180.000,rk2=53.21, rk3=53.21/
&rst iat=1489,15,14,0
r1=-180.00000,r2=66.38281,r3=66.38281,r4=180.000,rk2=40.55, rk3=40.55/
&rst iat=1490,1477,1489,15,0
r1=-180.00000,r2=11.03062,r3=11.03062,r4=180.000,rk2=29.83, rk3=29.83/
&rst iat=1477,1489,15,14,0
r1=-180.00000,r2=30.50819,r3=30.50819,r4=180.000,rk2=62.83, rk3=62.83/
&rst iat=1489,15,14,16,0
r1=-180.00000,r2=-137.04995,r3=-137.04995,r4=180.000,rk2=49.20, rk3=49.20/
Tip
The rest.in file should look familiar to you if you are familiar with Amber’s NMR restraint format, as Boresch restraints are implemented using the same underlying machinery.
Specifically, each &rst block in the rest.in file corresponds to a specific restraint type (distance, angle, dihedral) and contains the necessary parameters for that restraint.
You can tell what type of restraint it is based on the number of atoms involved:
Distance restraints involve 2 atoms
Angle restraints involve 3 atoms
Dihedral restraints involve 4 atoms
So the first line in rest.in is a distance restraint, since iat=1489,15
Now, the line after the &rst marker specifies the restraint values. Specifically, the fields always are:
r1: the lower bound where the restraint should reach infinity
r2: a mid-point of the restraint well where it should start taking effect (on its way to r1)
r3: another mid-point of the restraint well where it should start taking effect (on its way to r4)
r4: the upper bound where the restraint should reach infinity
rk2: the force constant for the left side of the well (between r1 and r2)
rk3: the force constant for the right side of the well (between r3 and r4)
Note
In between r2 and r3, there is no force applied (though, here you’ll note for all restraints r2=r3, meaning the well is harmonic in all cases.)
With these boresch restraints generated, you are now ready to use them in your ABFE calculations!