Comparing the PMF at the semi-empirical and ab initio level

Erika McCarthy1, Şölen Ekesan1, and Darrin M. York1
1Laboratory for Biomolecular Simulation Research, Institute for Quantitative Biomedicine and Department of Chemistry and Chemical Biology, Rutgers University, Piscataway, NJ 08854, USA

Learning objectives

  • Visualize the progression of the minimum free energy path on a free energy surface from a 2D reaction within MTR1

Relevant literature

Comparing the PMF at the semi-empirical and ab initio level

Insert Download link

The inputs should be copied to your working directory in a new folder called compare_PMF.

[user@cluster] mkdir compare_PMF
[user@cluster] cd compare_PMF
[user@cluster] cp -r /expanse/projects/qstore/amber_ws/tutorials/QMMM_DFTB3_MTR1/2D/compare_PMF/inputs/* ./

In this tutorial you have used an approximate semi-empirical Hamiltonian, so now let’s get a sense of how well it performed by comparing the PMF to the ab initio, PBE0 level PMF. This PMF was also generated using the string method. You have been provided a file called DFTB3.dat and PBE0.dat in the compare_PMF directory. DFTB3.dat is path file that we previously obtained when analyzing the DFTB3 strings that converged to the minimum free energy path.

Plot the DFTB3 and gwTP corrected PBE0 level PMF’s using xmgrace:

xmgrace -block DFTB3.dat -bxy 2:5 -block PBE0.dat -bxy 2:5

Align the PMFs such that the free energy is 0 at x=0 for both curves. This can be done in the Evaluate expression window under Data -> Transformations.

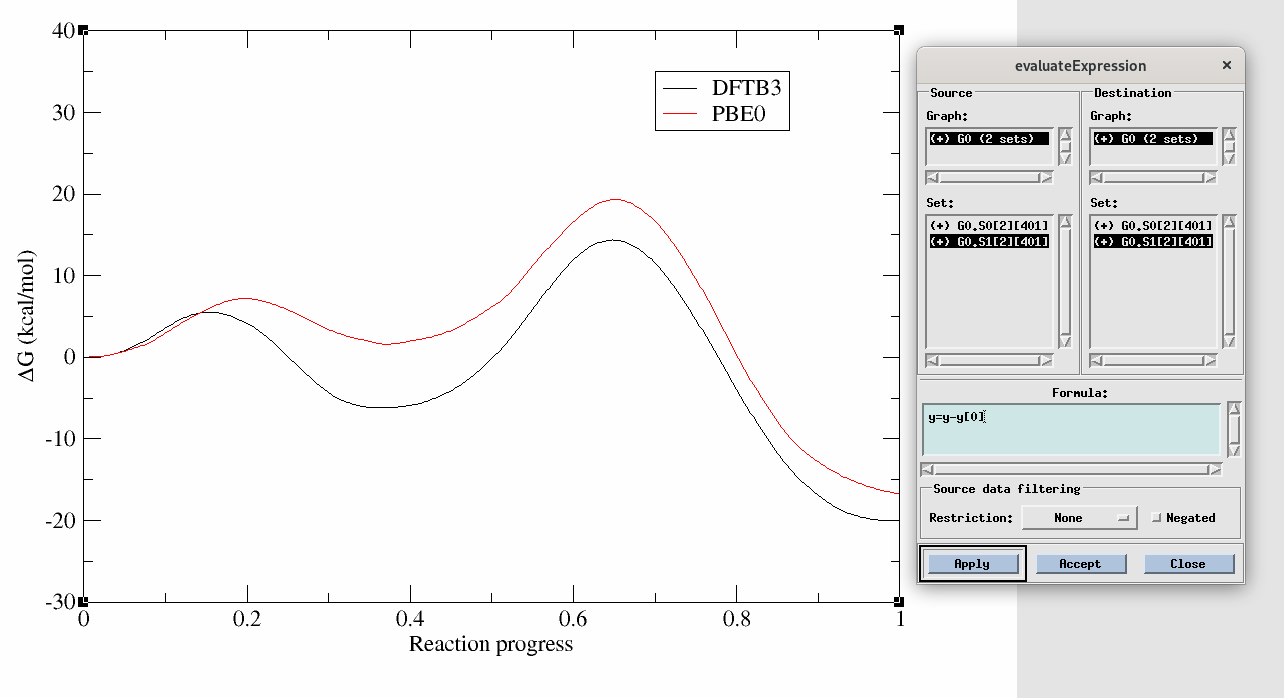
Figure 11

Figure 11. PMF as a function of reaction progress at the DFTB3 (black) and PBE0 (red) level of theory. The evaluate expression window demonstrates how to align the zero of energy for direct comparison.

Not only are the rate determining free energy barriers different, but the mechanistic interpretation is different when the higher level of theory is used. At the DFTB3 level (black) there is a stable intermediate state in which the proton transfer has occurred. This would suggest a proton would reside on the ligand a majority of the time. This is contrary to experimental activity-pH profiles of this type of base pair. At the PBE0 level (red), the intermediate is slightly higher in energy than the reactant state, suggesting the proton would likely be in rapid equilibrium between the cytosine residue and the ligand. This has implications for how one would interpret experimental observables such as pH dependence and highlights the importance of balancing the speed of the simulations with the accuracy of Hamiltonian.

References

  • McCarthy, E.; Ekesan, Ş; Giese, T. J.; Wilson, T. J.; Deng, J.; Huang, L.; Lilley, D. J.; York, D. M. Catalytic mechanism and pH dependence of a methyltransferase ribozyme (MTR1) from computational enzymology. Nucleic Acids Res. 2023, 51, 4508-4518 (10.1093/nar/gkad260)

  • Giese, T. J.; Ekesan, Ş; McCarthy, E.; Tao, Y.; York, D. M. Surface-Accelerated String Method for Locating Minimum Free Energy Paths. J. Chem. Theory Comput. 2024, 20, 2058– 2073 ( 10.1021/acs.jctc.3c01401)

  • Giese, T. J.; Ekesan, Ş; York, D. M. Extension of the Variational Free Energy Profile and Multistate Bennett Acceptance Ratio Methods for High-Dimensional Potential of Mean Force Profile Analysis. J. Phys. Chem. A 2021, 125, 4216– 4232 (10.1021/acs.jpca.1c00736)

  • Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931– 948 (10.1021/ct100684s)